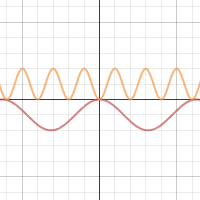
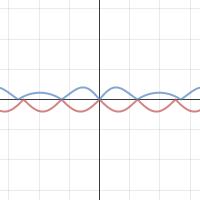
I’m reading through Measurement by Paul Lockhart these days. He presents math as something that you just need to “get messy with”. And moreover, suggests that we get messy together in asking ourselves challenging problems and developing clever arguments.
Consider this an attempt at heeding Lockhart’s advice.
Today I asked the following question on twitter.
Can two periodic functions intersect a finite number of times? #mathchat
— Geoff Krall (@emergentmath) February 18, 2013
And, to clarify, I mean continuous, differentiable periodic functions. Your sines, your cosines.
After that came a flurry of answers and conversations from all your favorite mathtwitterblogosphere partipants.
@emergentmath Or how about: f(x) = cos(x) – 1 and g(x) = 1 – cos(π*x). Only equal at 0.
— Joshua Bowman (@Thalesdisciple) February 18, 2013
.@emergentmath “Can 2 periodic functions intersect finitely many times?” Answer via @desmos: desmos.com/calculator/cwp… #mathchat #math
— Patrick Honner (@MrHonner) February 18, 2013
Here’s Patrick’s desmos graph:
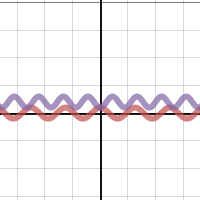
So definitely you can have a pair of periodic functions with one intersection. Initially I was wary of even this, but Joshua has me convinced. All you need is one of the periodic functions to have an irrational period (say, pi) and the other to have a rational period (say, 1) and both to be oppositely shifted vertically and the twain may meet just once.
- f(x)=cos(x)-1
- g(x)=cos(πx-π)+1
Also helpful, was this video from Joshua on irregular periods. Seeing this through the lens of rotating motion certainly helped me. It makes sense that something rotating with an irrational period will never match up with something rotating with a rational period more than once, if at all. After all, you can’t add a certain number of √2 ‘s together and get an integer. Easy peasy.
But I’m still wary of the existence a pair of periodic functions with two and only two intersections. In my head, a periodic function is one that satisfies the following:
f(x)=f(x+P) for all values of x and some constant P.
I’m trying to figure out how you’d make two functions meet within one period twice, and then never again. Here’s my attempt at a formal proof.
================================
If we assume that there are two solutions to the periodic functions f(x)=g(x), then we assume that,
g(a)=f(a)
and
g(a+c)=f(a+c) where c is some real number.
However, according to the definition of a periodic function, this would mean that
g(a+c+P)=g(a+c)=f(a+c) <— third (and presumably, infinite more) solutions!
================================
I could be wrong here. I’m not particularly moved by my own argument. If someone finds a couple periodic functions that do intersect more than 1 but less than infinity times, let us know in the comments or share your desmos.com graph. Or even better, make a more convincing argument (for or against) than I did.
Stay tuned, this post could probably get updated thanks to the collective brainpower of people that are much more clever than me.
================================
Update #1
Sure enough, I’m incorrect and my intuition was wrong. Check out this beauty from Dave (@daveinstpaul):
To see the functions used, click on the image.
So that’s three intersections. There’s still some hesitation here and on twitter as to whether you can have additional finite number of intersections. Keep looking and “getting messy” everyone!
And I would echo Joshua’s comment:
This was a fun discussion for a Monday. Thanks! RT @emergentmath On intersecting periodic functions wp.me/p1jLi5-in
— Joshua Bowman (@Thalesdisciple) February 19, 2013