Why would we design all problems and facilitation in a similar way without having the type of problem identified?
It’s possible I’ve been a bit too broad-brush when describing Problem Based Learning (PrBL) in terms of task design and facilitation. I’m beginning to wonder if we need a taxonomy of problems. After all, every problem implemented in a classroom will have different intended outcomes which can affect the design and facilitation of the task. After a while, you start to notice the similarities and patterns that like problems attend to. You also notices the differences. What I have not encountered, thus far, is a way of classifying the problems, which I think would make it easier to design, facilitate and assess. Once you have the problem type identified, that may allow you to use different tools, templates, rubrics, etc. around which the task may be designed.
Maybe it would be better if I just got to it. Consider this an attempt at Problem Taxonomy.
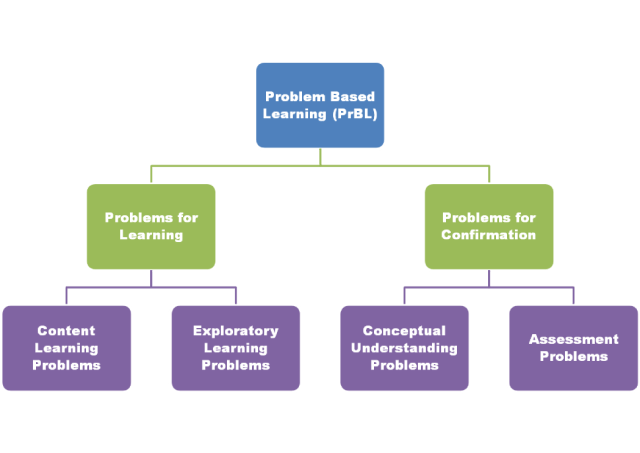
The four types of problems:
Problems for Learning/Constructing New Knowledge
These are problems that foster new knowledge within students.
Content Learning Problems
These are problems that have a predetermined, content-oriented outcome. Most of the time, this is what is often meant by Problem Based Learning. Or at least, it’s what I’ve basically meant in the past. Content Learning Problems are directly tied to a specific standard or standards. Scaffolding is often planned by the teacher ahead of time. Students work collaboratively and plan, strategize, struggle, and are coached toward a solution with the aid of the teacher. These may take 1-3 days.
Exploratory Learning Problems
These are problems that may foster new knowledge within students, but there is not a specific content standard tied to it. Although, Mathematical Practice standards, such as those defined in the Common Core, or Bryan’s Habits of a Mathematician truly shine in this type of problem. The solution and solution route may be unknown by the teacher. Related, the teacher may not have the scaffolding planned or predetermined until the need is made manifest. There is no prescribed method toward a solution and collaborative groups may have differing solutions and solution routes. These may take 1-5 days. Some may even call these “projects”.
Problems for Confirmation
These are problems intended to stand by themselves with minimal assistance or facilitation by the teacher. Students are to demonstrate the knowledge they have gained through Problems for Learning. I should note that, despite the naming convention, these problems don’t necessarily preclude learning opportunities.
Conceptual Understanding Problems
These are where a student puts the pieces together and begins to speak fluently about the content. If there was any confusion about the mathematical concept before, it’ll get crushed here. The scaffolding is quite intentionally student-centered with the specific intention of getting students to discuss the mathematics. Possibly the problem itself is more purely mathematical, or at least along the Skynet Line. Technology such as Geogebra investigations may be involved in order to solidify reasoning. These may take roughly a day or two.
Assessment Problems
Don’t tell the school district I worked for, but I once gave a single problem for my final exam of the year. It was a problem adapted from one of the Dana Center’s Assessments. I said, basically, “here’s your problem, you have two hours to show me what you’ve got. Now go!” The subtext of which was, “according to district rules, this single problem will count for 25% of your grade for the semester.” That’s basically what this kind of problem entails. Possibly solved individually, these problems are tied directly to content, require some decoding, and offer a chance for all to excel. I’d doubt there would be a presentation involved. Ideally (unlike in the scenario I described above), there would be some formative feedback or revision process before a numerical grade is attached. The point is, these are problems where students should know the content involved and be able to explain it with great fluidity.
=================================
So what do you think? Does this taxonomy work for you? Obviously the fine Art of Teaching necessitates that many of these types of problems overlap and intermingle. But in the design of a task, it’s important that you determine exactly what the outcomes should be. Are you constructing new mathematical knowledge within your students? Are you offering a place of creativity and non-linear thinking? Are you solidifying knowledge (Jo Boaler refers to this as “compression”)? Are you assessing understanding? Until you answer these questions, I’d suggest you can’t really fully develop the task.
In the next post, I’ll talk about what and ways to assess each of these types of problems.