emergent math

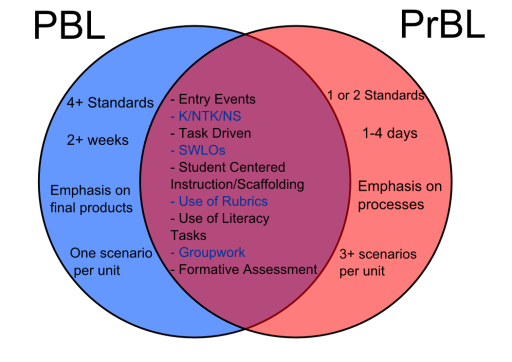
About a year ago, I started advocating and pushing towards a Problem Based approach in mathematics, as opposed to a solely Project Based approach, which many/most of my peers currently employ. But before we go any further, let’s better parse the differences between Project- (PBL) and Problem-Based Learning (PrBL). I realize that different people define and implement Problem and Project Based learning wildly differently. Some things I would define as problems, others would define as projects, and vice versa. So here’s what I mean by Problem and Project Based Learning:

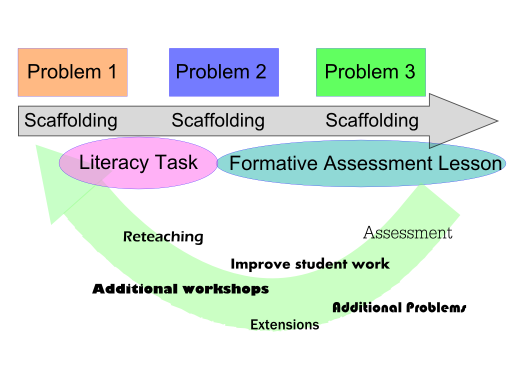
Pick your favorite diagram.

Figure 1.

Figure 2.

Figure 3 (sorry for the word- and acronym-slaw in this one).

The primary differences are size, scope, and end product. And then also a particular mathematical concept may require several problem scenarios instead on just one project scenario. Here are some untruths and half-truths I’ve heard about moving toward a Problem Based approach. I’d say the two hallmarks of PrBL (in my head at least) are as follows: 1) Each problem is about 1-4 days long and 2) the problem scenario comes first, the instruction and scaffolding succeeds the scenario.

Here are some misconceptions about Problem Based Learning. Let’s do this “Real or not real” style, since the Hunger Games is so popular with you kids.

“Problem Based Learning represents a step back in giving students authentic mathematical experiences.”

Not real. Maybe we need to define what is an “authentic mathematical experience.” A mathematical experience to me is something that promotes mathematical habits of mind. I’m totally going to steal from Bryan here (@doingmath) and point you towards his thinking through mathematical habits of mind. I’d argue that a problem can better facilitate the many of the mathematical habits of mind.

“Problem Based Learning is easier to facilitate than PBL.”

Not real. Due to the tighter time frame, a PrBL Math teacher always has to be formatively assessing students, differentiating instruction and generating good problems. You don’t have weeks to create a workshop, you have a day or so. So you either have to be well prepared for any and all student knowledge gaps and/or quick to respond to Need-to-Knows from students. To me, the work of PrBL is more challenging.

“Problem Based Learning allows teachers to be more ‘traditional’ in their facilitation.”

Not real. Like in PBL, the teacher acts more as a coach or facilitator, rather than a primary source/gatekeeper of knowledge. Students are still given a fair amount of autonomy in their problem solving strategies. Also, lectures still suck.

“Problem Based Learning is more about the math content, whereas PBL is more about 21st Century Skills.”

Sort of real. While I do believe PrBL can mesh nicely with 21st Century Skills, I am acknowledging of the fact that it does promote math content knowledge more than, say, writing a position article for a local newspaper. The fact is that by having the end product be a Socratic dialog among students rather than, say, a powerpoint presentation, may promote math content more than 21C Skills.

“Problem Based Learning is better for students who require more math remediation.”

Not real. In fact, I’d suggest that PrBL is exceptionally appropriate for advanced math courses such as Calculus. PrBL does tend to strip away some of the “psuedo-context” that often makes the math hidden within the weeds of a scenario.

“Problem Based Learning is better for novice teachers, or teachers new to an inquiry-based approach.”

Not real. As I mentioned earlier, PrBL is more work, more difficult, and requires higher order mathematical thinking and content knowledge and skills. It also requires teachers to always be on the lookout for a good math problem. It enhances your mathematical “spidey-sense”.

“If I’m teaching a mathematical concept, I have to make the choice to use either PBL or PrBL; it’s one or the other.”

Not real. There’s no reason a mixture of problems and projects, where each are appropriate, may be used. I would just caution to really think about your Projects: is the time spent in product refinement really enhancing mathematical understanding? Or is it just time spend doing “cool stuff?”

“Problem Based Learning doesn’t allow for authentic real world connections.”

Not real. The main differences are in the size and scope of the undertaking. Here are some or my problem ideas that take 1-4 days that have real world applications:

• Congressional State of the Union Seating
• U-Haul Linear Systems Problem
• Pizza Casbah 30-Inch Pizza Challenge
• The Geometry of Gerrymandering
• Rainbow Robot Art
• Building a Soccer Goal
• The Mavericks Complaining About Officiating
• A Edgy Brownie Pan

For more, I’d highly recommend Brian Marks’ awesome YummyMath.

However, I will concede that PrBL does allow for the use of non-real-world connections, and promote pure mathematical conceptual understanding, whereas a Project really sort of needs to be couched in some real-world product. My follow-up question: is it really such a bad thing if the math has nowhere to hide in a problem?

“In Problem Based Learning, students are just given a problem and expected to work through it on their own.’”

Not real. This might be a misconception about PBL in general: that students are just supposed to “figure it out” or that the teacher isn’t expected to “teach” as much. This is flat out incorrect or improper implementation of PBL and PrBL. Every problem ought to have some form of scaffolding along with it. Maybe it’s a lecture, maybe it’s one of these tasks, maybe it’s students sharing their solution route ideas and then going forward as a class. While students are expected to begin to attempt a solution without initial handholding, the facilitator is still expected to address Need-to-Knows with some sort of scaffolding. And the teacher is also responsible for getting students off on the right foot by facilitating some sort of strategizing and brainstorming process.

“You don’t really assess problems in the same way as you do projects.”

Sort of real. I suppose this is more personal preference, but there’s no reason you can’t assess the a problem in the same way you can a project. The main difference is that it might be impractical to develop, say, a full, zillion rowed and columned rubric every couple days. However, the practice of using a rubric to assess across multiple skills and proficiencies is still an excellent practice (despite what others have suggested) . So, a suggestion:

• Develop one rubric per unit, or batch of problems. Focus on a couple or one particular key learning outcome aside from Math content. For example, written communication: have students have some sort of writing component in every problem for a couple weeks and use the same rubric, or the same written communication component of that rubric.

One other note about assessment for now: I’d suggest it’s easier to assess something like Critical Thinking through the use of a Problem rather than a Project. In a Project, you summatively assess the final, polished product. In a problem, all that scratchwork, brainstorming, and multiple solution attempts are right there on the paper. I’m saying it’s any easier to assign a numerical score to Critical Thinking, just that it can be more evident in Problem Based Learning.

“Non-math teachers can’t help me refine my problems.”

Not real. If anything, I’d suggest non-math teachers are particularly adept at helping you refine your problems. Often, math teachers become so insular and like-minded we can see what the problem is trying to get at. We’re particularly adept at sifting through “psuedo-context” to find out what problems are really asking, while other teachers (and, ultimately, our students) may not be. So by enlisting their support, either by Critical Friend-ing or by actually facilitating the Need-to-Know process, you’ll probably get a better idea of what the problem will look like in an actual real-live class with real-live students instead of a bunch of math teachers.

========================================

What misconceptions have you head about Problem Based Learning that I/we can address in the comments?