Let’s say you’re teaching a Grade 8 or Freshman level class. Algebra 1-ish. You’ve got some data here.
| x | y |
| 1 | 3 |
| 2 | 5 |
| 4 | 10 |
| 6 | 10 |
| 8 | 12 |
| 10 | 17 |
You want to show how data may be modeled as an equation. We could go about this two ways.
We could follow some TI-84 instructions via a handy dandy set of instructions.
We could also do something like this in Desmos, using the sliders feature.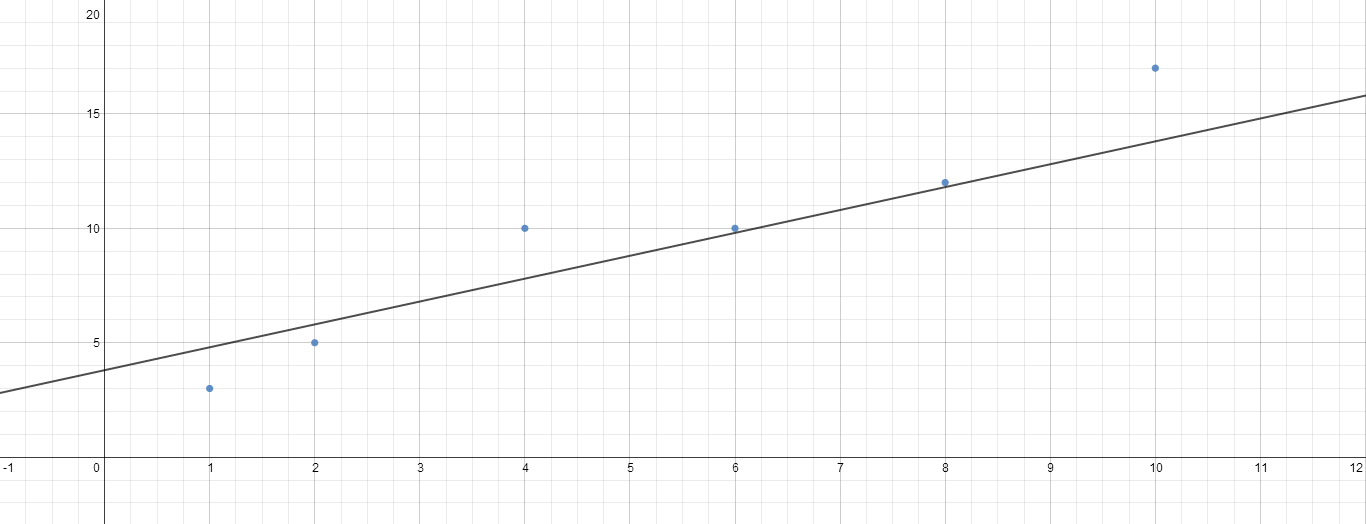
Students would be asked to manipulate the sliders until they think they have the line of best fit.
Discussion questions:
- Which of these activities leads to the more accurate answer?
- Which of these develops a better understanding of how a data set may be represented by an equation?
I wouldn’t say that conceptual understanding and accuracy are always juxtaposed, but it seems that they sure can be. I think I’ll leave it at that for now, but I’m a bit terrified to pursue this line of thinking much further. There might be drastic implications that I’m not sure I’m emotionally ready to handle right now.
emergent math 