While I intend to make a longer, “My Semester with Desmos” post in the near future, I wanted to prime the pump by writing about the saving grace of the Activity Builder feature in Amplify’s Desmos platform: the ability to create self-checking exercises. I’ll have plenty to discuss on why I’m calling this the “saving grace” because while there were a lot of positives in using AB for College Algebra and Developmental Math, there are a few massive drawbacks. But, according to my students, the self-checking features (which I had to learn to code as the semester went along) were a huge boon.
There’s some trepidation around self-checking exercises. Two common criticisms I see are as follows:
- What’s the difference between self-checking AB exercises, and, say, some other platform like Khan Academy’s practice exercises?
- It puts an emphasis on correctness over process.
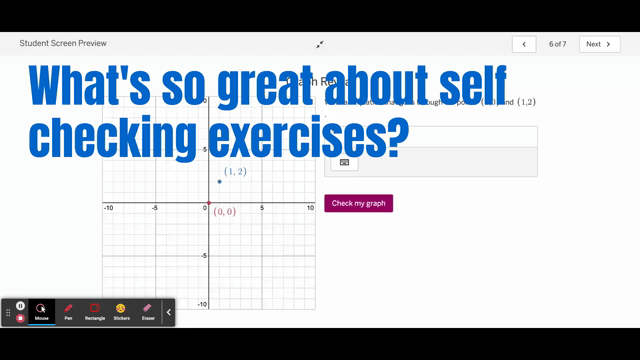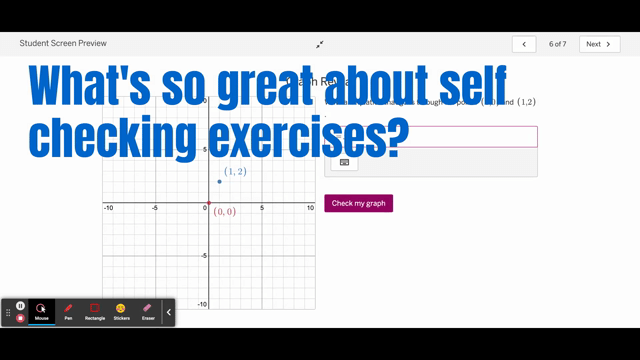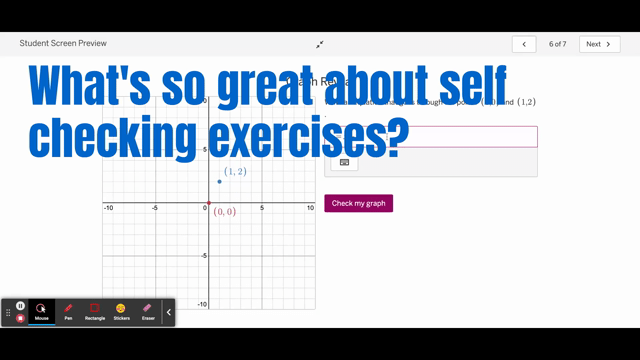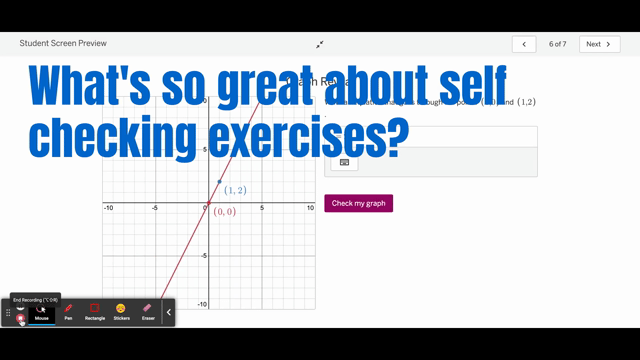
To address the first issue, I suppose there isn’t a ton of difference between (some) AB self-checking exercises and other digital platforms. Shucks, it’s not that much different than checking your answer in the back of the book! However, I am able to control the problem and control the response. I am able to create various types of check-as-you-go exercises: matching, numerical answers, graph reveal, etc. Most KA are multiple choice or numerical.
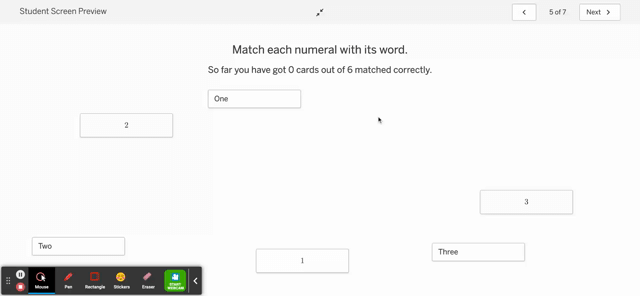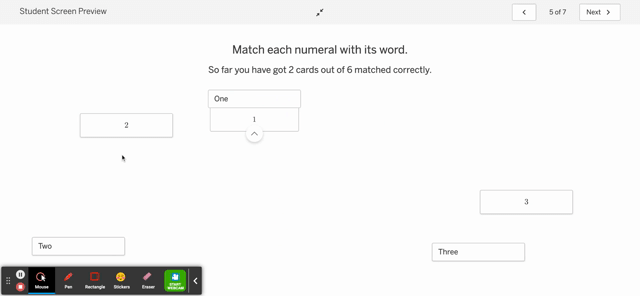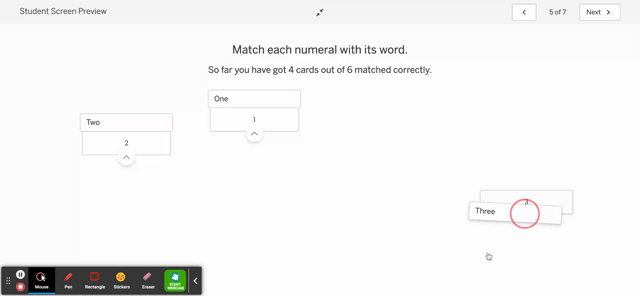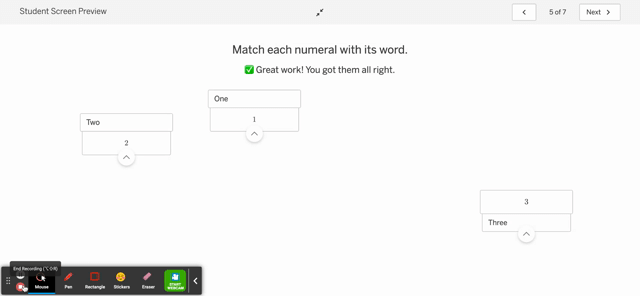
I’m also able to personalize it with, oh, I dunno, a fun .gif. I suppose that’s just window dressing, but it is delightful.
And – and this is going to preview my general “My Semester with Desmos” post, the biggest value-add in Desmos Activity Builder is, and always has been, and always will be the calculator. Desmos was built on its calculator and to this day, it still remains the best feature Desmos has to offer. Desmos AB’s most important asset is that it is synced with the Desmos calculator. That’s something that no other digital math platform can offer.
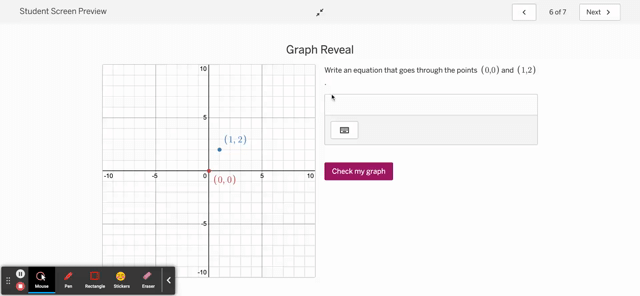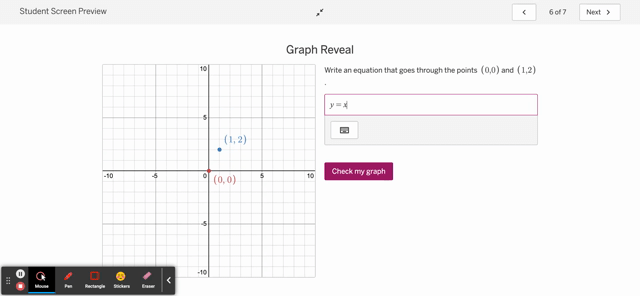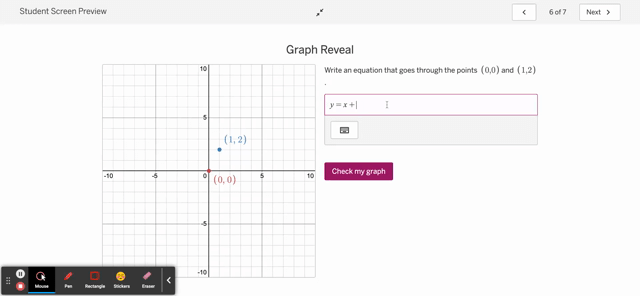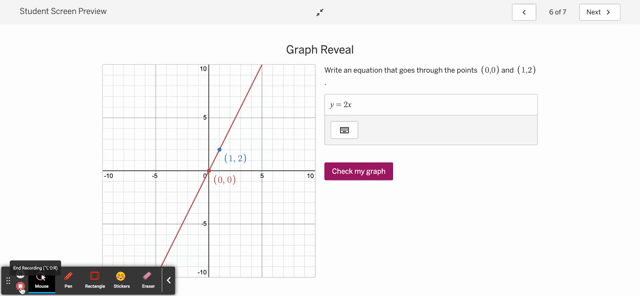
As for the second issue on correctness, I’m going to be bold and say it’s ok if a student is told they are incorrect on something provided, the student can go back and correct the issue in a low- or no-stakes manner. That’s ok, and frankly, what I’d want a student to take away from my class: not that they don’t make mistakes, but that they can correct their mistakes.
Dan provides nice examples of assessment modes that are better than correct/incorrect. No disagreement that these are generally better. They are also a level of Computation Layer learning that simply isn’t worth it for me. At least not now, not in the middle of lesson planning. Yes, I want to generate as many activities as possible that reveal and probe student thinking. And rest assured, we do that. There are other times when we as mathematicians work alone and at-our-own-pace or in small workshop groups where it’s ok if students move on to the next problem (assuming they understand the prior problem).
So what’s so great about self-checking exercises anyways?
Well, I asked my students about halfway through the semester. Several of them mentioned that was their favorite part of Desmos AB. Here are three of their responses, accompanied by a bit of additional commentary from Yours Truly.
“It allows me to know immediately if I got it right or not.” Students don’t have to wait for a discussion or probing questions. They can know right away. Good feedback is timely, and there’s nothing more timely than instantaneous.
“It’s not a big deal if I get something wrong.” One of the things I appreciate is the low-stakes nature of Desmos AB. I’m glad Amplify has resisted requests to integrate grading features into Desmos. I fully concur that they don’t belong, would represent mission creep, and bleed into some pretty questionable teaching practices. Because of that, a self-checking exercise is genuinely no big deal if a student gets something wrong. Because it’s instantaneous and on-screen, and accompanied by a friendly note, getting something wrong isn’t a day-ruiner.
“I can do it on my own if I’m not in class.” One of the many issues I have with Desmos (again, a future post) is that it assumes the ideal class conditions: 100% attendance with no school distractions, replete with perfectly timed lessons that fill the class time. Unfortunately, real classrooms rarely operate like that: students are absent, lessons go long or short. This is doubly true of a College Algebra course that meets once a week. If a student misses a class’s activities, they can negotiate their way through it with the guardrails of self-checkingness.
Lessons steeped in student-to-student discourse are ideal and I want to spend as much class time in that mode as possible. That isn’t an option if a student is unable to be in class due to illness, extracurriculars, or suspension. Self-checking exercises allow for asynchronous work in a way that Desmos activities typically aren’t (which I believe is a feature, not a bug).
***
If you’re interested in kicking the tires on some self-checking exercises and templates (perhaps over the upcoming Winter break) you can check out the google doc I created of some self-checking samples and template as well as this copy-pastable set of slides.
In the next few weeks, I intend to continue to process this semester including describing additional positives and the aforementioned drawbacks of Desmos’ AB. If I have the time and capacity, I may even tackle the metaphysical question, what exactly is College Algebra (what are we doing here)?