Author: Geoff
-

We’re about to get a lot of dubious research on A.I. in education
Education journals are calling for papers on AI, but educators have barely even had access to it. So what kind of research on AI are we going to see in 2024?
-

Experiencing novice-ness through tabletop games
It’s important as seasoned Math teachers we remember what it’s like to experience new content. Modern tabletop games might be the best way to create those experiences.
-

My semester with Desmos Activity Builder
This semester I taught College Algebra and Developmental Math at a community college. Being new to the institution, I mostly hewed to the standards and progressions and textbooks from prior iterations of the course taught by more tenured faculty. However, I did make one significant change: the graphing calculator. While previous iterations of the course…
-
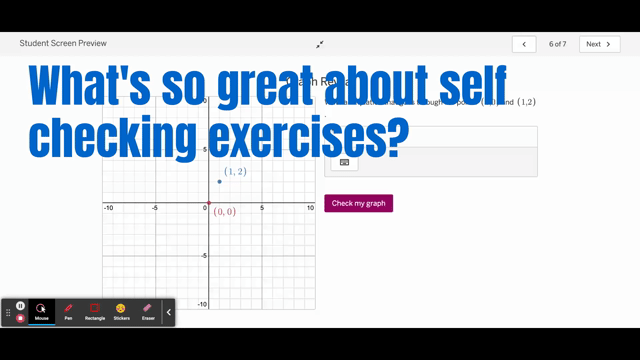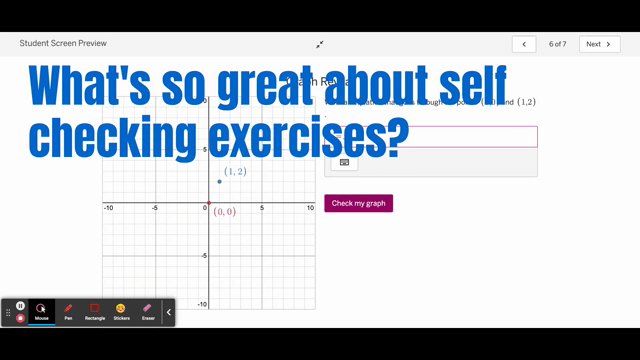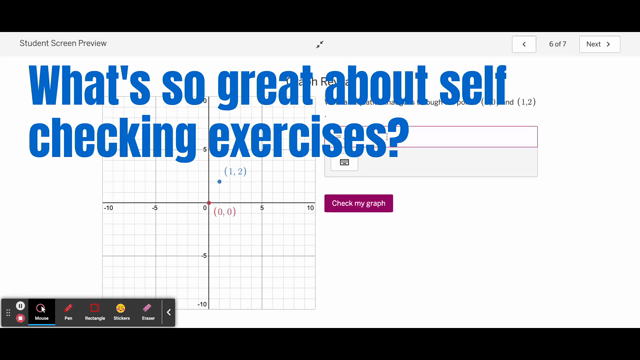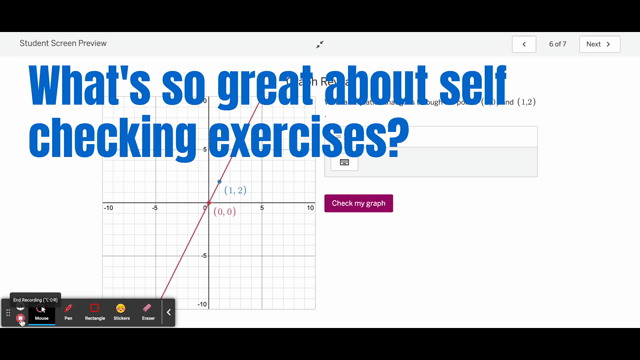
What’s so great about self-checking exercises?
My students really appreciated self-checking exercises this semester iin College Algebra. This post offers some benefits and examples of self-checking exercises using Desmos’ Activity Builder feature.
-

‘Necessary Conditions’ Five Years Later
Necessary Conditions was published five years ago this Fall. I’m not sure if five years is a long time or a short time, but it’s a natural time frame to reflect on the book (since we evolved to have five fingers instead of, say, four). So I apologize in advance for what is sure to…
-

Reconceptualizing “more math” for pre- and in-service teachers
I am rereading Liping Ma’s Knowing and Teaching Elementary Mathematics for a class. It’s an exceptional book; I’d put it on the Mount Rushmore of books about math education (that might be a post for another day). For those who haven’t read it, the book is an exploration of elementary math instruction in the U.S.…
-
No pushback: So I guess education has given up
In 2019, North Carolina attempted to push through a bill that would force trans individuals to use the bathroom of their sex assigned at birth, rather than their current gender. It was only a few years ago, but there was mass outrage in a way that seems unthinkable today. Most notably, the National Basketball Association…
-
Is the Subway Footlong Pass Worth It?
This post is for all you Italian BMT heads out there. For the month of April 2023, Subway customers have the option of purchasing a “Subway Footlong Pass” for $15. You then get 50% off all (I think) Subway sandwiches for the month (digital orders only). Please don’t look down on me, but I get…
-

A few reasons to teach, learn, and do math
As you may have heard, adults don’t need or use math. One can be a successful human without being a successful math learner. In fact, most adolescents and young adults will stop taking mathematics as soon as their school no longer requires them to do so. So why do we force adolescents and young adults…